
As I mentioned earlier, this can be decomposed into the problem of moving. To check the implementation in C programming, click here. In this case, the first function wants to move N disks from rod A to rod C via rod B. Hanoi(disk - 1, aux, dest, source) // Step 3 How do we do this By recursively using the same procedure.

Hanoi(disk - 1, source, aux, dest) // Step 1 Move disks 4 and smaller from peg A (source) to peg C (spare), using peg B (dest) as a spare. The steps to follow are − Step 1 − Move n-1 disks from source to aux Step 2 − Move n th disk from source to dest Step 3 − Move n-1 disks from aux to destĪ recursive algorithm for Tower of Hanoi can be driven as follows − We can imagine to apply the same in a recursive way for all given set of disks. Our ultimate aim is to move disk n from source to destination and then put all other (n1) disks onto it. The largest disk (n th disk) is in one part and all other (n-1) disks are in the second part. We divide the stack of disks in two parts. So now, we are in a position to design an algorithm for Tower of Hanoi with more than two disks.
and a procedure Move(k, f rom, to) to move the top k (1 in.

We mark three towers with name, source, destination and aux (only to help moving the disks).
#MOVE METHOD HANOI TOWERS HOW TO#
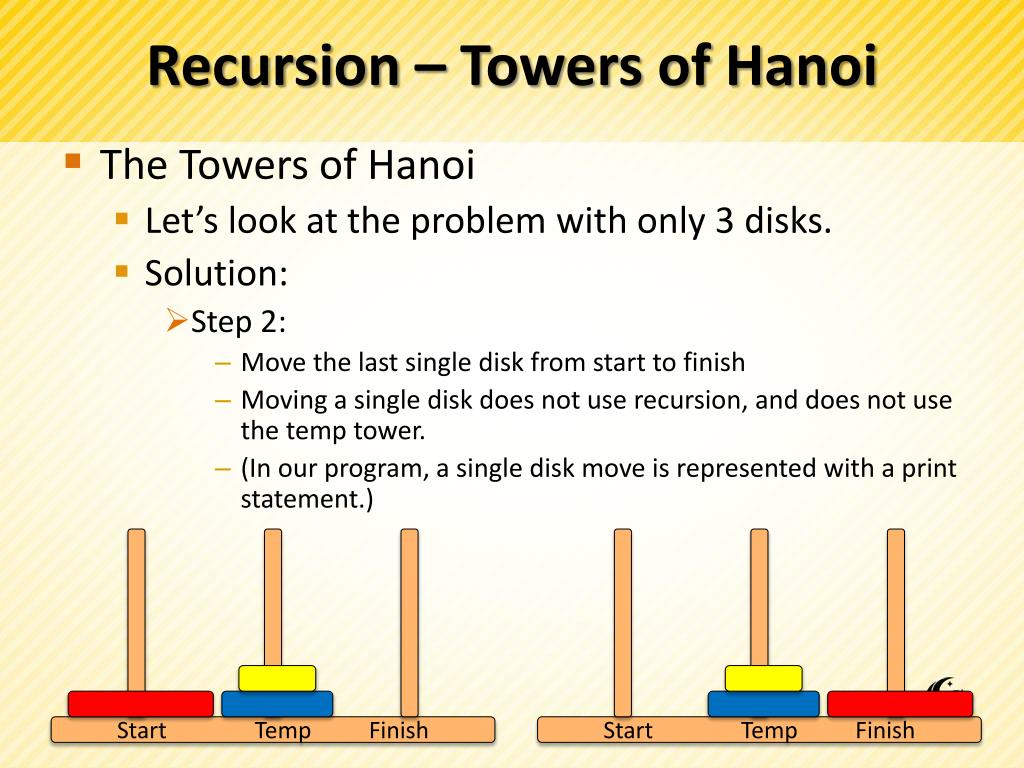
To write an algorithm for Tower of Hanoi, first we need to learn how to solve this problem with lesser amount of disks, say → 1 or 2. This presentation shows that a puzzle with 3 disks has taken 2 3 - 1 = 7 steps. Tower of Hanoi puzzle with n disks can be solved in minimum 2 n−1 steps. No large disk can sit over a small disk.įollowing is an animated representation of solving a Tower of Hanoi puzzle with three disks.To solve a 1-disk Tower of Hanoi, simply move the disk from post A to post C. Only one disk can be moved among the towers at any given time. The simplest form of the Tower of Hanoi puzzle has only 1 disk.A few rules to be followed for Tower of Hanoi are −
#MOVE METHOD HANOI TOWERS SERIES#
The mission is to move all the disks to some another tower without violating the sequence of arrangement. There are three poles in a row, the one on the left containing a series of discs of decreasing size, with the other two, empty. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same. the smaller one sits over the larger one. These rings are of different sizes and stacked upon in an ascending order, i.e. We can imagine to apply the same in a recursive way for. Remember that only the top disk requires to be removed. Our ultimate aim is to move disk n from source to destination and then put all other (n1) disks onto it. Basic programming knowledge is necessary as some quizzes require programming in Python.Tower of Hanoi, is a mathematical puzzle which consists of three towers (pegs) and more than one rings is as depicted − What is Tower of Hanoi A person only has to move one disk amid towers at a specific period.

We assume only basic math (e.g., we expect you to know what is a square or how to add fractions), common sense and curiosity.Ģ. In the online course, we use a try-this-before-we-explain-everything approach: you will be solving many interactive (and mobile friendly) puzzles that were carefully designed to allow you to invent many of the important ideas and concepts yourself.ġ. We will use these tools to answer typical programming questions like: How can we be certain a solution exists? Am I sure my program computes the optimal answer? Do each of these objects meet the given requirements? In this course, we will learn the most important tools used in discrete mathematics: induction, recursion, logic, invariants, examples, optimality. Consider a two-disk game were I want to move 2 disks from tower 0 onto. Mathematical thinking is crucial in all areas of computer science: algorithms, bioinformatics, computer graphics, data science, machine learning, etc. I can now use this method to write an algorithm for solving the Towers of Hanoi game.


 0 kommentar(er)
0 kommentar(er)
